Deterministic Finite Automata VS Nondeterminic Finite Automata

Hingga Otomat dapat diklasifikasikan menjadi dua jenis -

• Deterministic Finite Automaton (DFA)
• Finite Automaton Non-deterministik (NDFA / NFA)

Deterministic Finite Automaton (DFA)

Dalam DFA, untuk setiap simbol input, seseorang dapat menentukan status kemana mesin akan bergerak. Oleh karena itu, itu disebut Deterministic Automaton . Karena memiliki sejumlah negara terbatas, mesin ini disebut Deterministic Finite Machine atau Deterministic Finite Automaton.

Definisi Resmi DFA

DFA dapat diwakili oleh 5-tupel (Q, ∑, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut alfabet.
• δ adalah fungsi transisi di mana δ: Q × ∑ → Q
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).
• F adalah seperangkat status akhir / status Q (F ⊆ Q).

Representasi grafis dari DFA

DFA diwakili oleh digraf yang disebut diagram keadaan .

• Verteks mewakili negara.
• Busur berlabel alfabet input menunjukkan transisi.
• Keadaan awal dilambangkan dengan satu busur masuk yang kosong.
• Keadaan akhir ditunjukkan oleh lingkaran ganda.

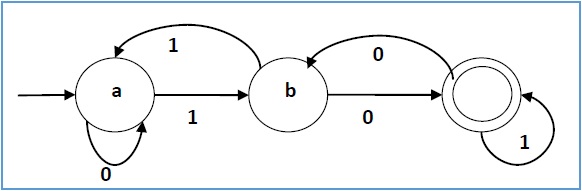
Contoh

Biarkan otomat terbatas deterministik menjadi →

• Q = {a, b, c},
• ∑ = {0, 1},
• q 0 = {a},
• F = {c}, dan

Fungsi transisi δ seperti yang ditunjukkan oleh tabel berikut -

Keadaan saat ini	Status Selanjutnya untuk Input 0	Status Selanjutnya untuk Input 1
Sebuah	Sebuah	b
b	c	Sebuah
c	b	c

Representasi grafisnya adalah sebagai berikut -

Dalam NDFA, untuk simbol input tertentu, mesin dapat berpindah ke kombinasi status apa pun di dalam mesin. Dengan kata lain, kondisi pasti tempat mesin bergerak tidak dapat ditentukan. Oleh karena itu, itu disebut Non-deterministic Automaton . Karena memiliki jumlah negara hingga, mesin ini disebut Mesin Hingga Non-deterministik atau Non-deterministic Finite Automaton .

Definisi Resmi suatu NDFA

NDFA dapat diwakili oleh 5-tupel (Q,, δ, q 0 , F) di mana -

• Q adalah seperangkat status terbatas.
• ∑ adalah seperangkat simbol terbatas yang disebut huruf.
• δ adalah fungsi transisi di mana δ: Q × ∑ → 2 Q
  (Di sini set daya Q (2 Q ) telah diambil karena dalam kasus NDFA, dari suatu keadaan, transisi dapat terjadi pada kombinasi dari keadaan Q)
• q 0 adalah kondisi awal dari mana input diproses (q 0 ∈ Q).
• F adalah seperangkat status akhir / status Q (F ⊆ Q).

Representasi Grafis dari NDFA: (sama seperti DFA)

NDFA diwakili oleh digraf yang disebut diagram keadaan.

• Verteks mewakili negara.
• Busur berlabel alfabet input menunjukkan transisi.
• Keadaan awal dilambangkan dengan satu busur masuk yang kosong.
• Keadaan akhir ditunjukkan oleh lingkaran ganda.

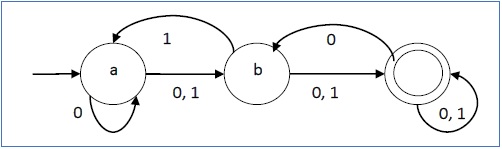
Contoh

Biarkan otomat hingga non-deterministik menjadi →

• Q = {a, b, c}
• Β = {0, 1}
• q 0 = {a}
• F = {c}

Fungsi transisi δ seperti yang ditunjukkan di bawah ini -

Keadaan saat ini	Status Selanjutnya untuk Input 0	Status Selanjutnya untuk Input 1
Sebuah	a, b	b
b	c	a, c
c	b, c	c

Representasi grafisnya adalah sebagai berikut -

DFA vs NDFA

Tabel berikut mencantumkan perbedaan antara DFA dan NDFA.

DFA	NDFA
Transisi dari keadaan adalah ke keadaan berikutnya tunggal khusus untuk setiap simbol input. Karena itu disebut deterministik .	Transisi dari status dapat ke beberapa status berikutnya untuk setiap simbol input. Karena itu disebut non-deterministik .
Transisi string kosong tidak terlihat di DFA.	NDFA mengizinkan transisi string kosong.
Mengulangi diizinkan dalam DFA	Di NDFA, mundur tidak selalu mungkin.
Membutuhkan lebih banyak ruang.	Membutuhkan lebih sedikit ruang.
Suatu string diterima oleh DFA, jika transit ke keadaan akhir.	Sebuah string diterima oleh NDFA, jika setidaknya satu dari semua transisi yang mungkin berakhir dalam keadaan akhir.

Akseptor, Klasifikasi, dan Transduser

Akseptor (Pengenal)

Otomat yang menghitung fungsi Boolean disebut akseptor . Semua status akseptor menerima atau menolak input yang diberikan padanya.

Penggolong

Sebuah classifier memiliki lebih dari dua negara akhir dan memberikan satu output ketika berakhir.

Transduser

Otomat yang menghasilkan output berdasarkan input saat ini dan / atau keadaan sebelumnya disebut transduser . Transduser dapat terdiri dari dua jenis -

• Mesin Mealy - Output tergantung pada kondisi saat ini dan input saat ini.
• Moore Machine - Output hanya tergantung pada kondisi saat ini.

Penerimaan oleh DFA dan NDFA

Sebuah string diterima oleh DFA / NDFA jika DFA / NDFA dimulai dari keadaan awal berakhir pada keadaan penerima (salah satu dari status akhir) setelah membaca string sepenuhnya.

String S diterima oleh DFA / NDFA (Q,, δ, q 0 , F), iff

δ * (q 0 , S) ∈ F

Bahasa L yang diterima oleh DFA / NDFA adalah

{S | S ∈ ∑ * dan δ * (q 0 , S) ∈ F}

String S ′ tidak diterima oleh DFA / NDFA (Q,, δ, q 0 , F), iff

δ * (q 0 , S ′) ∉ F

Bahasa L ′ tidak diterima oleh DFA / NDFA (Pelengkap bahasa yang diterima L) adalah

{S | S ∈ ∑ * dan δ * (q 0 , S) ∉ F}

Contoh

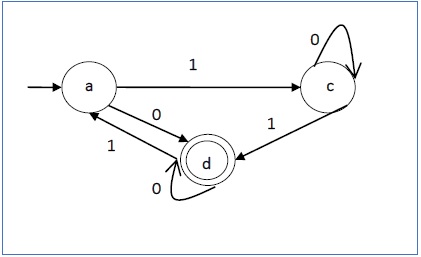
Mari kita perhatikan DFA yang ditunjukkan pada Gambar 1.3. Dari DFA, string yang dapat diterima dapat diturunkan.

String diterima oleh DFA di atas: {0, 00, 11, 010, 101, ...........}

String tidak diterima oleh DFA di atas: {1, 011, 111, ........}

Pernyataan masalah

Misalkan X = (Q x , ∑, δ x , q 0 , F x ) menjadi NDFA yang menerima bahasa L (X). Kita harus merancang sebuah DFA setara Y = (Q y , Σ, δ y , q 0 , F y ) sehingga L (Y) = L (X) . Prosedur berikut mengubah NDFA ke DFA yang setara -

Algoritma

Input - Sebuah NDFA

Output - DFA yang setara

Langkah 1 - Buat tabel negara dari NDFA yang diberikan.

Langkah 2 - Buat tabel keadaan kosong di bawah abjad input yang mungkin untuk DFA yang setara.

Langkah 3 - Tandai status awal DFA dengan q0 (Sama seperti NDFA).

Langkah 4 - Cari tahu kombinasi States {Q 0 , Q 1 , ..., Q n } untuk setiap alfabet input yang memungkinkan.

Langkah 5 - Setiap kali kita menghasilkan status DFA baru di bawah kolom alfabet masukan, kita harus menerapkan langkah 4 lagi, jika tidak, lanjutkan ke langkah 6.

Langkah 6 - Negara-negara bagian yang berisi negara bagian terakhir NDFA adalah negara bagian terakhir dari DFA yang setara.

Contoh

Mari kita perhatikan NDFA yang ditunjukkan pada gambar di bawah ini.

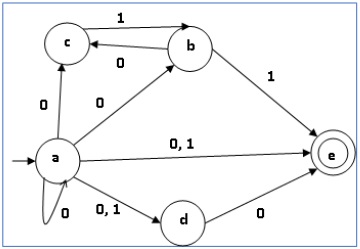
q	δ (q, 0)	δ (q, 1)
Sebuah	{a, b, c, d, e}	{d, e}
b	{c}	{e}
c	∅	{b}
d	{e}	∅
e	∅	∅

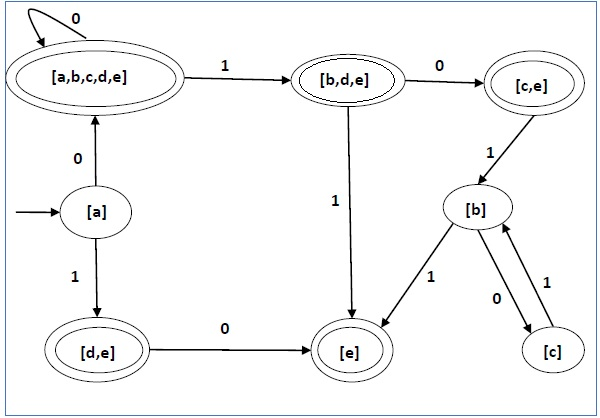
Dengan menggunakan algoritma di atas, kami menemukan DFA yang setara. Tabel status DFA ditunjukkan di bawah ini.

q	δ (q, 0)	δ (q, 1)
[Sebuah]	[a, b, c, d, e]	[d, e]
[a, b, c, d, e]	[a, b, c, d, e]	[b, d, e]
[d, e]	[e]	∅
[b, d, e]	[c, e]	[e]
[e]	∅	∅
[c, e]	∅	[b]
[b]	[c]	[e]
[c]	∅	[b]

Diagram keadaan DFA adalah sebagai berikut -